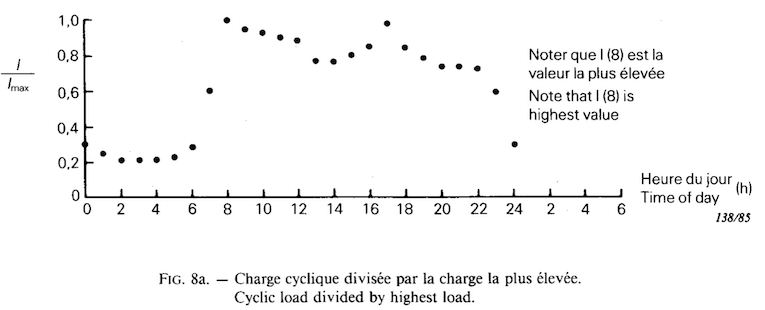
The load factor is the ratio between the average power (the energy supplied to the system) and the maximum demand in a period of time. For example, the daily load cycle will be calculated from the average hourly power demands $P_i$, the maximum average hourly power demand $P_{max}$ and a duration $i_{max}$ of 24 hours.
The load factor is usually obtained with energy and demand measurements. Seasonal load and load growing may be considered. The consumer diversity and the different consumer behaviours in areas with different geographical and socioeconomic characteristics may also influence the load factor.
When the demand and the energy are related, the load factor is important for evaluating the economics of any supply. Given that a system is planned as a function of the maximum demand, a high load factor means a high use rate and, consequently, reduced unitary cost (for unit of supplied energy).
For cables in air, channel or tunnel, steady-state load is typically considered. You may use a load factor for the quadratic mean method as described in the book 'Kabel und Leitungen für Starkstrom' by L. Heinhold, 5th edition 1999 (in German). But please note that with this method it is not possible to calculate the maximal permissible current at a certain temperature but instead it is used to calculate the reduction in temperatures in comparison to steady-state when a load factor is applied.
For buried cables, the load factor can be changed between 0.5 and 1.0.