Cableizer ®

Thermal resistance medium in the duct

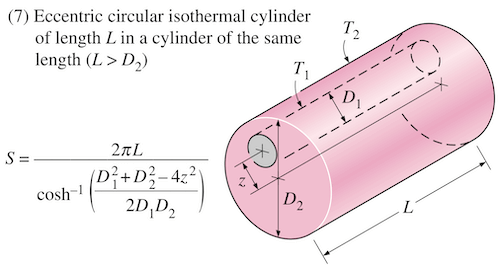
The equation for ducts with bentonite filling is based on the conduction shape factor of a cylinder surrounded by an eccentric cylinder of larger radius, refer to Table 5.4 in the book 'A Heat Transfer Textbook' by John H. Lienhard IV and V (Phlogiston Press 2008) or to table 3.5 in the book 'Heat Transfer - A Practical Approach' by Yunus A. Cengel (2014). It is assumed that the cables are in the duct so that it comes to contact.

Symbol
$T_{4i}$
Unit
K.m/W
Formulas
$\frac{U_{d}}{1+0.1\left(V_{d}+Y_{d} \theta_{dm}\right) D_{eq}}$Default
$\frac{\rho_{d,fill}}{2\pi} \cosh^{-1}\left(\frac{{Di_{d}}^2+{D_{eq}}^2-\left(\frac{Di_{d}}{2}-\frac{D_{eq}}{2}\right)^2}{2Di_{d} D_{eq}}\right)$Bentonite filling, steady-state
$\frac{\theta_{e}-\theta_{di}}{W_{conv,og}-W_{conv,gd}+W_{rad,int}}$Cables in riser
$\frac{\theta_{e}-\theta_{di}}{W_{conv,int}+W_{rad,int}}$Cables in riser Chippendale
$\frac{1}{\frac{\pi D_{eq}}{1000} \left(h_{conv,int}+h_{rad,int}\right)}$Cables in riser IEC 60287
$F_{\alpha} T_{4i}$buried inclined ducts
$\frac{1}{\frac{D_{e}}{1000} \left(a_{d} \left(\frac{\theta_{di} {p_{gas}}^2}{\frac{D_{e}}{1000}}\right)^{\frac{1}{4}}+b_{d}+c_{d} \theta_{dm}\right)}$Neher-McGrath 1957
Related
$a_{d}$
Constant a for cables in ducts
$b_{d}$
Constant b for cables in ducts
$c_{d}$
Constant c for cables in ducts
$D_{e}$
External diameter object [mm]
$D_{eq}$
Equivalent diameter of a group of round objects [mm]
$Di_{d}$
Inner diameter duct [mm]
$F_{\alpha}$
Inclination derating factor [p.u.]
$h_{conv,int}$
Heat transfer coefficient convection cable—riser [W/(K.m$^2$)]
$h_{rad,int}$
Heat transfer coefficient radiation cable—riser [W/(K.m$^2$)]
$p_{gas}$
Pressure gas [Pa]
$\pi$
Archimedes' constant $\pi$
$\rho_{d,fill}$
Thermal resistivity duct filling [K.m/W]
$\theta_{di}$
Temperature duct inner surface [°C]
$\theta_{dm}$
Mean temperature medium in the duct [°C]
$\theta_{e}$
External temperature object [°C]
$U_{d}$
Constant U for cables in ducts
$V_{d}$
Constant V for cables in ducts
$W_{conv,gd}$
Convective heat transfer gas—duct [W/m]
$W_{conv,int}$
Convective heat transfer cable→riser [W/m]
$W_{conv,og}$
Convective heat transfer cable→gas [W/m]
$W_{rad,int}$
Radiation heat transfer cable—riser [W/m]
$Y_{d}$
Constant Y for cables in ducts
Used in
$\Delta \theta_{c}$
Temperature rise conductor [K]
$\Delta \theta_{d}$
Temperature rise dielectric losses [K]
$I_{c}$
Conductor current [A]
$Q_{B,ab}$
Thermal capacitance B transient thermal circuit, armour bedding [J/(m.K)]
$Q_{B,d}$
Thermal capacitance B transient thermal circuit, duct [J/(m.K)]
$Q_{B,f}$
Thermal capacitance B transient thermal circuit, filler [J/(m.K)]
$Q_{B,j}$
Thermal capacitance B transient thermal circuit, jacket [J/(m.K)]
$T_{4ss}$
Thermal resistance steady-state [K.m/W]
$T_{B}$
Thermal resistance B transient thermal circuit [K.m/W]
$T_{eq}$
Thermal resistance, equivalent [K.m/W]
$T_{r}$
Thermal resistance, total [K.m/W]
$\theta_{di}$
Temperature duct inner surface [°C]
$\theta_{e}$
External temperature object [°C]
$U_{wall}$
OHTC pipe wall [W/(K.m$^2$)]
Image

Heat Transfer - A Practical Approach by Yunus A. Cengel (2014) Table 3-5