The calculation of thermal resistances of the internal components of cables for single-core cables is straightforward. However, the calculations of two- and three-core cables are more complicated and rigorous mathematical formulas cannot be determined, but mathematical expressions to fit the conditions have been derived. The general method employs geometric factor in place of the logarithmic term for single-core cables according to IEC 60287-2-1.
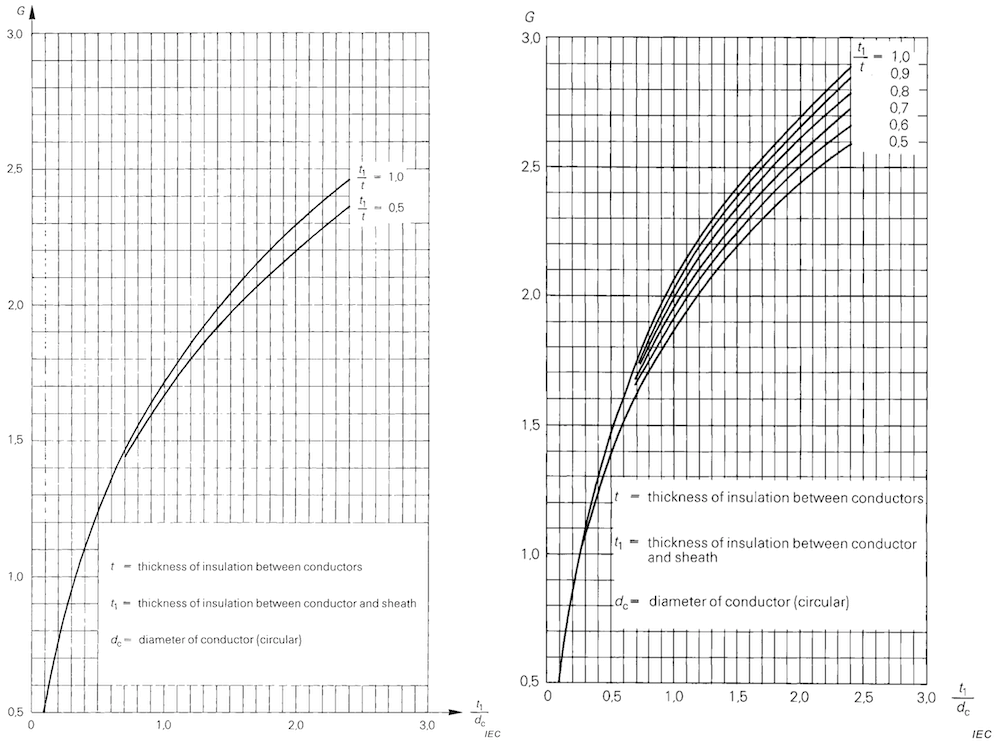
The quantity $G_1$ for two- and three-core cables with round conductors is given graphically in IEC 60287-2-1, Figure 2 and 3.
The IEC 60287 differs between two- and three-core belted (unscreened, low voltage) cables and three-core screened cables which have a separate screen over each core. Further differences are made between round and sector-shaped conductors.
| $\ln\left(C_{Mie}\right) K_G$ | Multi-core cables, round conductors |
| $\ln\left(1+\frac{2t_1}{d_c}\right)$ | Three-core cables, separate sheaths |
| $2\left(1+\frac{2.2t_{2i}}{2\pi \left(d_x+t_{2i}\right)-t_{2i}}\right) \ln\left(\frac{D_f}{d_c}\right)$ | Two-core cables, sector-shaped conductors |
| $3\left(1+\frac{3t_{2i}}{2\pi \left(d_x+t_{2i}\right)-t_{2i}}\right) \ln\left(\frac{D_f}{d_c}\right)$ | Three-core cables, sector-shaped conductors |
| $3\left(1+\frac{3t_{2i}}{2\pi \left(d_x+t_{2i}\right)-t_{2i}}\right) \ln\left(\frac{D_{sc}}{d_c}\right)$ | Three-core cables, sector-shaped conductors, screened |
| $\left(0.85+0.2\left(\frac{2t_1}{t_{2i}}-1\right)\right) \ln\left(\left(8.3-2.2\left(\frac{2t_1}{t_{2i}}-1\right)\right) \frac{t_1}{d_c}+1\right)$ | Three-core cables, round conductors (Simons1923) |
| $4\left(1+\frac{4t_{2i}}{2\pi \left(d_x+t_{2i}\right)-t_{2i}}\right) \ln\left(\frac{D_f}{d_c}\right)$ | Four-core cables, sector-shaped conductors |
| $5\left(1+\frac{5t_{2i}}{2\pi \left(d_x+t_{2i}\right)-t_{2i}}\right) \ln\left(\frac{D_f}{d_c}\right)$ | Five-core cables, sector-shaped conductors |