®
®
Calculations of pulling forces or pulling tensions for cable trays are similar to those for pulling cable in conduit, adjusting the coefficient of friction to reflect using rollers and sheaves.
If the sheaves in the bends in cable trays are well-maintained, they will not have the multiplying effect on the force that bends in conduit have. The sheaves will turn with the cable, allowing the coefficient of friction to be assumed zero. This results in the commonly-used approximation for conduit bend equation becoming one. Even though cable tray bends produce no multiplying effect, it is essential for heavier cables to include the force required to bend the cable around the sheave. If the sheaves are not well-maintained, the bend will have a multiplying effect. The pulling force must then be calculated using the same equations used for installations in conduit.
Pulling lubricants must be compatible with cable components and be applied while the cable is being pulled. Pre-lubrication of the conduit is recommended by some lubricant manufacturers.
The approximate results display only the pulling forces at the end of the respective sections, while the forward and backward direction tabs display the pulling forces all along the route. The approximate results also use a simplified equation for bends, which does not consider the gravitational forces or the vertical elevations.
The equation for a horizontal bend and the four equations for vertical bends are taken from CIGRE TB 194 (also found in TB 889). The equations originate from a publication by R. C. Rifenburg from 1953. The publication called 'Pipe-line design for pipe-type feeders' explains how the equations are derived through integration. In the paper following conditions were made which are not stated explicitly in CIGRE but which are relevant.
| $F_{pull}+F_g L_{leg} \left(sin\left(\phi_e\right)+\Kappa cos\left(\phi_e\right)\right)$ | straight section |
| $F_{pull} e^{\Kappa \phi_b}$ | bend (approximation) |
| $F_{pull} cosh\left(\Kappa \phi_b\right)+sinh\left(\Kappa \phi_b\right) \sqrt{{F_{pull}}^2+\left(F_g R_b\right)^2}$ | horizontal bend |
| $F_{pull} e^{\Kappa \phi_b}-\frac{F_g R_b}{1+{\Kappa}^2} \left(2\Kappa sin\left(\phi_b\right)-\left(1-{\Kappa}^2\right) \left(e^{\Kappa \phi_b}-cos\left(\phi_b\right)\right)\right)$ | concave vertical bend, pulling up |
| $F_{pull} e^{\Kappa \phi_b}+\frac{F_g R_b}{1+{\Kappa}^2} \left(2\Kappa e^{\Kappa \phi_b} sin\left(\phi_b\right)+\left(1-{\Kappa}^2\right) \left(1-e^{\Kappa \phi_b} cos\left(\phi_b\right)\right)\right)$ | convex vertical bend, pulling up |
| $F_{pull} e^{\Kappa \phi_b}+\frac{F_g R_b}{1+{\Kappa}^2} \left(2\Kappa sin\left(\phi_b\right)-\left(1-{\Kappa}^2\right) \left(e^{\Kappa \phi_b}-cos\left(\phi_b\right)\right)\right)$ | convex vertical bend, pulling down |
| $F_{pull} e^{\Kappa \phi_b}-\frac{F_g R_b}{1+{\Kappa}^2} \left(2\Kappa e^{\Kappa \phi_b} sin\left(\phi_b\right)+\left(1-{\Kappa}^2\right) \left(1-e^{\Kappa \phi_b} cos\left(\phi_b\right)\right)\right)$ | concave vertical bend, pulling down |
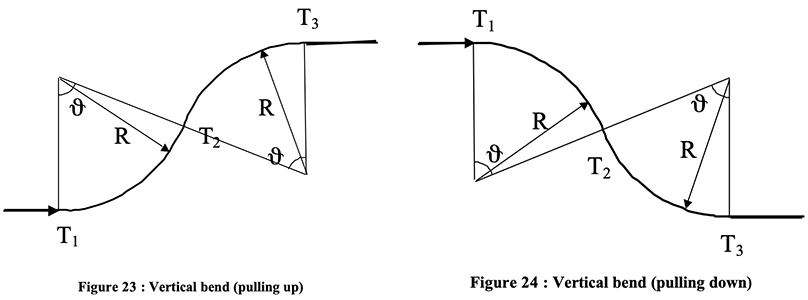
Vertical bends, Figure 23 + 24 - CIGRE TB 194 (2001)