The magnetic field is calculated based on the law of Biot-Savart where each subconductor is represented by a filament current extending along its axis.
The current for each phase at the time step $t_{EMF}$ is given as follows.
| $\sqrt{2} I_{c} cos\left(\omega t_{EMF}+\alpha_{f}\right)$ | 3-phase system with relative phase angle 120°, phase R (L1) |
| $\sqrt{2} I_{c} cos\left(\omega t_{EMF}-\frac{2\pi}{3}+\alpha_{f}\right)$ | 3-phase system with relative phase angle 120°, phase S (L2) |
| $\sqrt{2} I_{c} cos\left(\omega t_{EMF}+\frac{2\pi}{3}+\alpha_{f}\right)$ | 3-phase system with relative phase angle 120°, phase T (L3) |
| $\sqrt{2} I_{c} cos\left(\omega t_{EMF}+\alpha_{f}\right)$ | 2-phase system with relative phase angle 180°, phase U (L1) |
| $-\sqrt{2} I_{c} cos\left(\omega t_{EMF}+\alpha_{f}\right)$ | 2-phase system with relative phase angle 180°, phase V (L2) |
| $\sqrt{2} I_{c} cos\left(\omega t_{EMF}+\alpha_{f}\right)$ | Mono-phase system (L1) |
| $I_{c}$ | DC system, phase P (L1) |
| $-I_{c}$ | DC system, phase N (L2) |
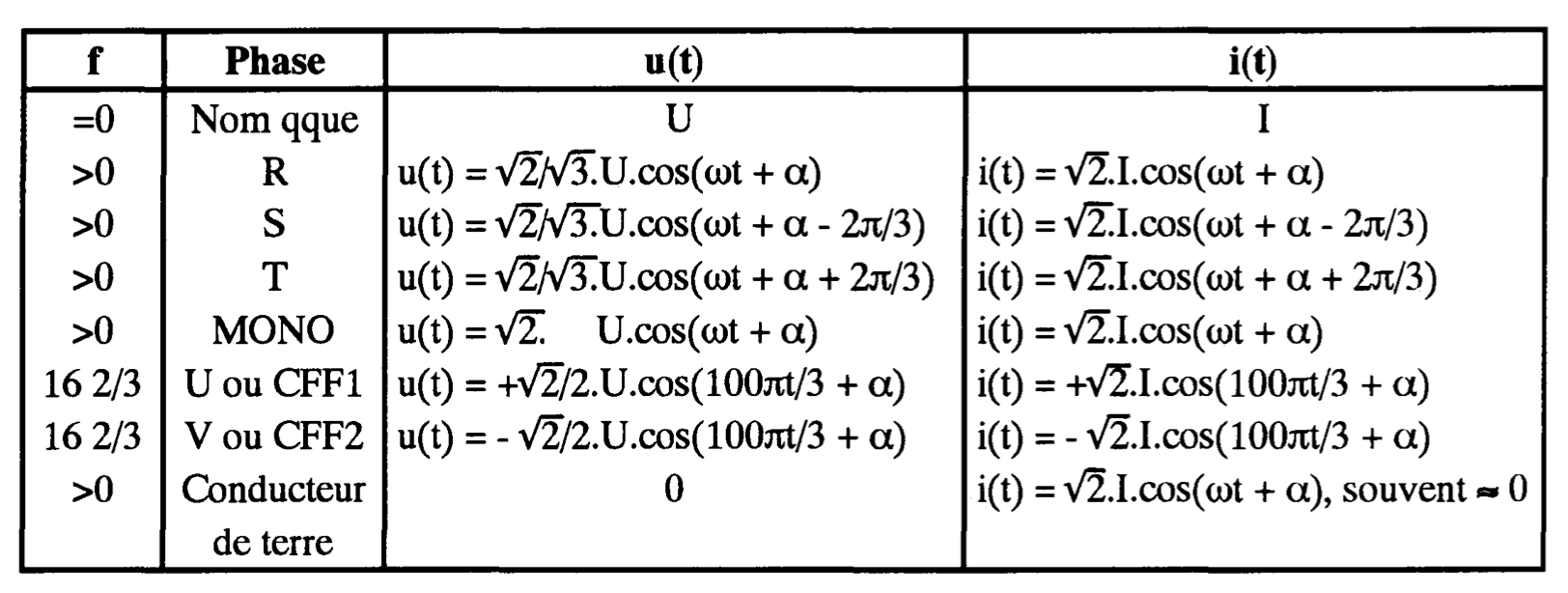
Définitions des tensions et des courants, Programme CHAMP, Dr. Pierre-André Chamorel (EPFL 1999)