Cableizer ®

Equivalent diameter of a group of round objects

For multiple cables twisted or bound together, a combined diameter circumscribing all cables can be calculated. The resulting value is also approximately correct for three loose cables in touching trefoil formation.

The equivalent diameter over the conductors for three core cables without a filler (not round), can be calculated by dividing the circumference with $\pi$. In case of three-core cables, they are called triplex; and in case of two-core cables we call them duplex. The equation is according to CIGRE TB 880 Guidance Point 48 while the circumference of such a cable is according to CIGRE TB 880 Guidance Point 41.

For multiple unequal round objects, possibly non-touching, finding the smallest circle that encompasses all other circles is not easy and we consider following approximation as presented in stackoverflow.com

  1. Take the average of all your centers of the circles call this point X
  2. Let R1 be the maximum distance from X to a circle center
  3. Let R2 be the maximum radius of the circles
  4. Then all the circles must fall inside the circle centered at X with radius R1+R2

For spaced ducts inside the air-filled pipe, the above method often results in a circle larger than the inner diameter of the pipe. So instead, we are using another approximation by summation of squared areas of all circular objects inside the pipe to get $A_{eq}$ and then $D_{eq} = \sqrt{A_{eq} / \pi}$.

Symbol
$D_{eq}$
Unit
mm
Formulas
$F_{eq} D_e$multiple cables
$\frac{n_c D_{shj}+\left(D_{shj}+2\left(t_{ab}+t_{ar}+t_j+t_{jj}\right)\right) \pi}{\pi}$duplex/triplex cable
$2.15D_{sc}$pipe-type cables with skid wires
$2.15D_{shj}$pipe-type cables with sheath jacket
$f{\left(\right)}$air-filled pipe with objects
Related
$D_e$
External diameter object [mm]
$D_{sc}$
Diameter over screen [mm]
$D_{shj}$
Diameter over sheath jacket [mm]
$f$
System frequency [Hz]
$F_{eq}$
Factor for envelope circle for a group of equal circles
$n_c$
Number of conductors cable
$\pi$
Archimedes' constant $\pi$
$t_{ab}$
Thickness armour bedding [mm]
$t_{ar}$
Thickness armour [mm]
$t_j$
Thickness jacket [mm]
$t_{jj}$
Thickness of additional layer over jacket [mm]
Used in
$T_{4d}$
Thermal resistance daily load cycle [K.m/W]
$T_{4i}$
Thermal resistance medium in the duct [K.m/W]
$T_{4pi}$
Thermal resistance of medium in the air-filled pipe with objects [K.m/W]
$T_{4w}$
Thermal resistance weekly load cycle [K.m/W]
$T_{4y}$
Thermal resistance yearly load cycle [K.m/W]
$T_{spf}$
Thermal resistance steel pipe filling [K.m/W]
Image

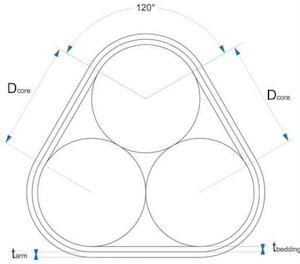
CIGRE TB 880 Guidance Point 41