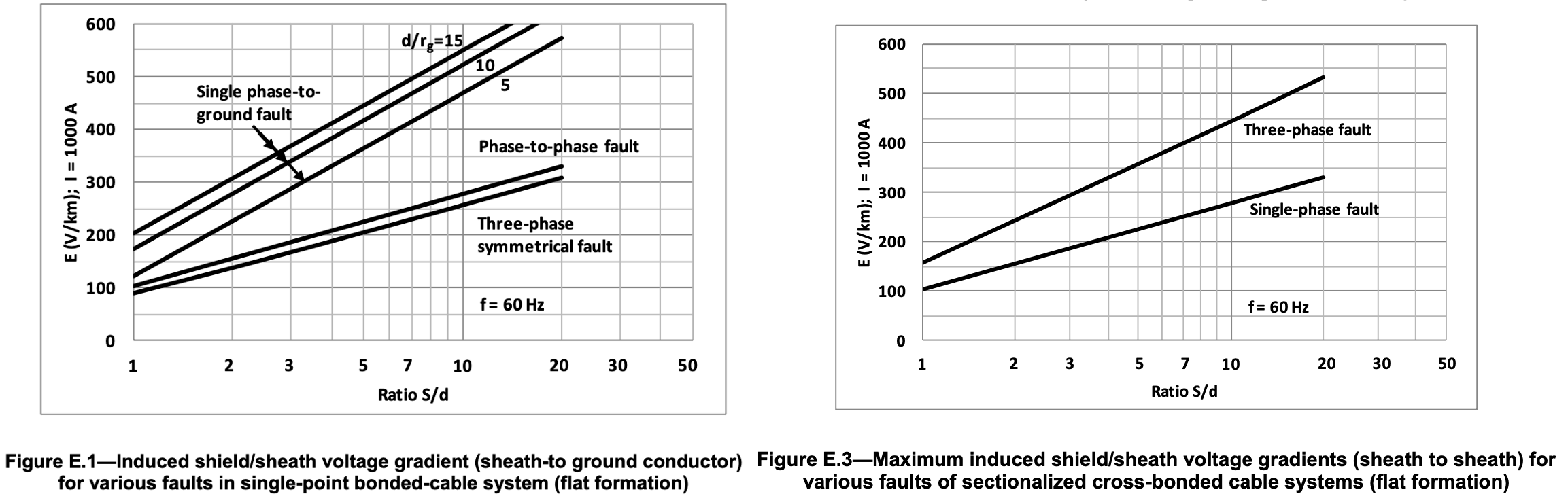
Typical maximum values of shield/sheath voltages calculated from these equations are given in Figure E.1 for a circuit in flat formation, for a current of 1000 A having a transposed ground conductor. For a three-phase symmetrical fault, the maximum voltage is reached in the outer cables. For the phase-to-phase fault, the highest shield/sheath voltage results when the fault is between the outer cables so that $S_{ac} = 2 \cdot S$.
The highest of the three-sheath voltages for a fault in phase a is $E_{a}$, and since the effect of $R_{c}$ can generally be neglected, the preceding equation for $E_{a}$ can be expressed as shown in the equation.
Figure E.1 shows the effect of varying $d/r_{g}$ over a typical range of values. It is clear that the overvoltages per meter due to the single-phase fault is much greater than for the other types of fault, for systems having solidly grounded neutral. For systems having impedance or resonant grounding of the neutral, the phase-to-phase fault is the most important.
Figure E.3 shows these voltages between shields/sheaths at the cross-bond position per unit length of 1 m of the minor section length calculated from the equations above for single-phase faults and compared with the voltages due to three-phase symmetrical faults and for phase-to-phase faults and for a short-circuit current of 1000 A. It is evident that the voltage due to the phase-to-phase fault is the greatest.
The shield/sheath voltage limiter generally consists of a star connected device having the star point grounded to a local ground. The resistance of these local ground plates is often high but some current will flow into the ground during a single-phase fault. The calculation of these currents and of the voltages between the shields/sheaths and the ground plates is complex and requires knowledge of the ground-plate resistances and the ground resistivity along the cable route. These values are not generally known, especially at the design stage, and hence it is usual to consider the duty of the shield/sheath voltage limiter only in terms of the voltage between shields/sheaths. Experience and measurements indicate that the shield/sheath-to-ground voltage rise is not generally sufficient to damage the shield/sheath voltage limiter, but, when there is any doubt, the star point should not be grounded, when this is permissible, with respect to transient overvoltages.
| $+j \omega I_{ka} 2{\cdot}{10}^{-7} \ln\left(\left(\frac{S_m}{d}\right)^2 \frac{d}{r_g}\right)$ | highest single-phase ground fault in phase a, single-side bonded |
| $+j \omega I_{kb} 2{\cdot}{10}^{-7} \ln\left(\left(\frac{S_m}{d}\right)^2 \frac{d}{r_g}\right)$ | highest single-phase ground fault in phase b, single-side bonded |
| $+j \omega I_{kc} 2{\cdot}{10}^{-7} \ln\left(\left(\frac{S_m}{d}\right)^2 \frac{d}{r_g}\right)$ | highest single-phase ground fault in phase c, single-side bonded |
IEEE 575 Magnitude of voltages