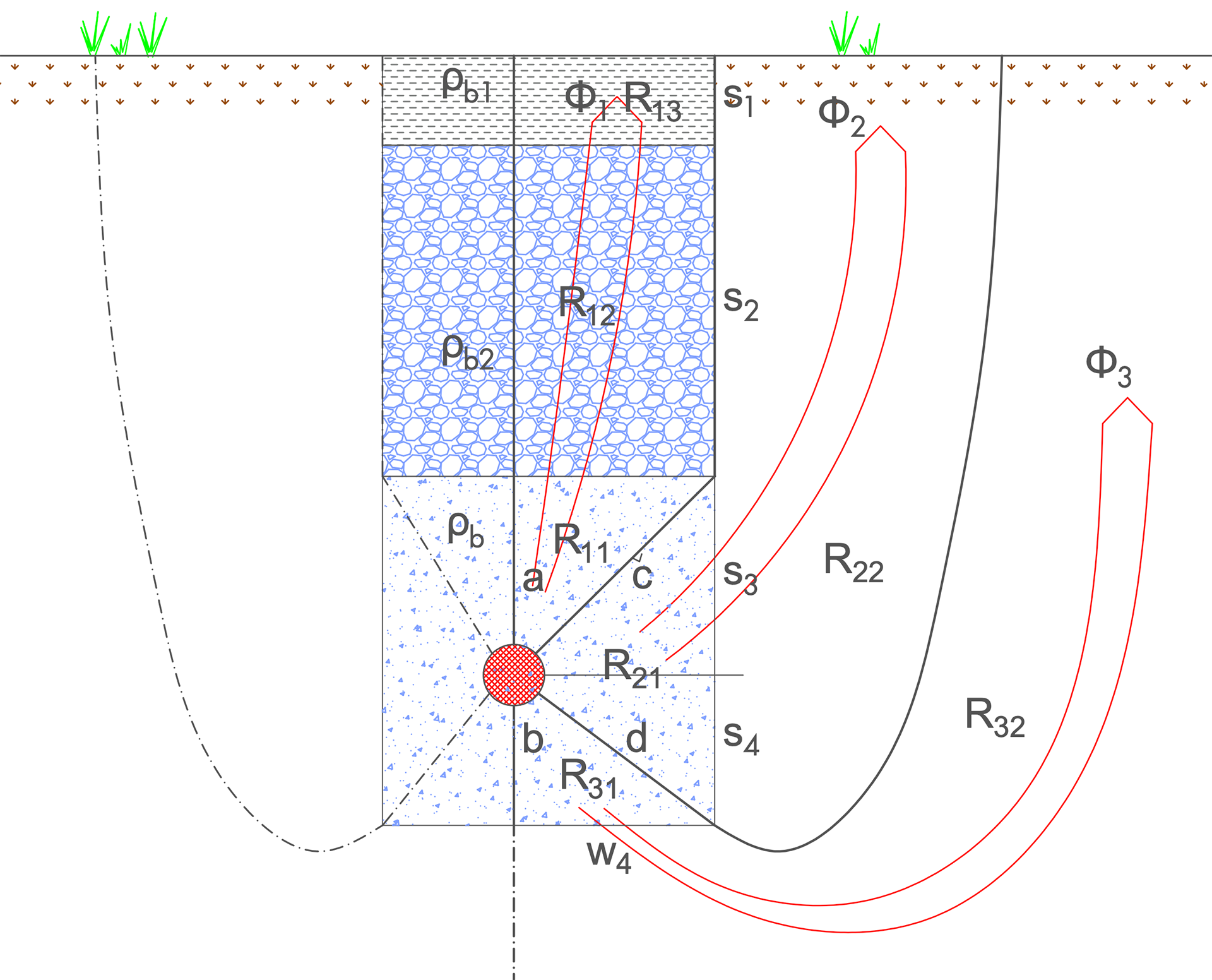
Overall thermal resistance between buried cables in a multi-layer backfill and the ground surface.
All resistances $R_q$ are calculated once for the side with shorter distance to the backfill boundary, and once for the other side. The resistances were defined in the paper by R. de Lieto Vollaro et.al: 'Experimental study of thermal field deriving from an underground electrical power cable buried in non-homogeneous soils', 2014.The total resistance to ambient $T_{4iii}$ is calculated by taking the two values of $R_{CG}$ for the two sides in parallel.
Range of variability of the controlling parameters:
| $s_{b1}$ [m] | $s_{b2}$ [m] | $s_{b3}$ [m] | $w_b$ [m] | $L_{b4}$ [m] | $L_{cm}$ [m] | $s_{b4}$ [m] | $w_b$/$L_{b4}$ | $ρ_{b1}$ [K.m/W] | $ρ_{b2}$ [K.m/W] | $ρ_{b}$ [K.m/W] | $ρ_{4}$ [K.m/W] | |
| min | 0.048 | 0.2 | 0.3 | 0.41 | 1.02 | 0.66 | 0.17 | 0.215 | 0.52 | 0.52 | 0.52 | 0.31 |
| max | 0.16 | 1.5 | 1.3 | 1.4 | 2.55 | 2.24 | 0.48 | 1.264 | 9.80 | 9.52 | 7.14 | 8.62 |
Within the range of variability as given in the paper by R. de Lieto Vollaro et.al: 'Thermal analysis of underground electrical power cables buried in non-homogeneous soils', 2011, the best fit of the numerical data for the overall thermal resistance $R_{CG}$ was derived by way of Montecarlo optimization method. The method has a 3.6 % standard deviation of error and a 10 % range of relative error with a 98 % level of confidence. The paper points out that if the trench is filled with a single backfilling material (i.e., $\rho_{b1}$ = $\rho_{b2}$ = $\rho_{b}$), which means that the method from IEC 60287 can be applied, the range of relative error of the results obtained through the IEC method is +/- 35 %. Whenever the trench is filled with layers of different materials stacked one above the other, the only possibility of application of the IEC 60287 is to replace the actual multiple filling of the trench with a single fictitious material having an equivalent thermal resistivity given by the weighted average of the thermal resistivities of the backfilling layers and the cable bedding, in which the weights are their thicknesses. In such case, the order of the errors is noticeably much higher with +250 / -45 % than that corresponding to the use of the multi-layer method.