Cableizer ®

Cable drum calculator

The cable drum calculator helps you to determine the length of cable of a certain type which fits onto a specific cable drum and it calculates the total weight.

Posted 2026-01-05
Categories: Tools

The cable drum calculator is based on a spreadsheet tool originally developed by the manufacturer Brugg Cables from Switzerland to calculate the capacity of a cable defined by its diameter on standard drums. In addition it also provided a method to calculate the capacity for user-defined drums which is what has been transformed to this tool.

With the input of the weight per meter of the cable it calculates also the total weight of the cable on the drum. And based on publicly available data for different drum sizes the weight of the user-defined empty drum is approximated in order to get the total weight of cable and drum, a useful information for a transport study.

What this code does

This code reads the current drum and cable dimensions from the user session, calculates how many cable windings and radial layers can fit on the drum, and then estimates the total cable length that can be wound onto the drum. It also computes the remaining unused space in width and radius.

All input dimensions are in millimeters (mm). The resulting cable length is in meters (m). The tool can also be used with US units.

Inputs (read from the session)

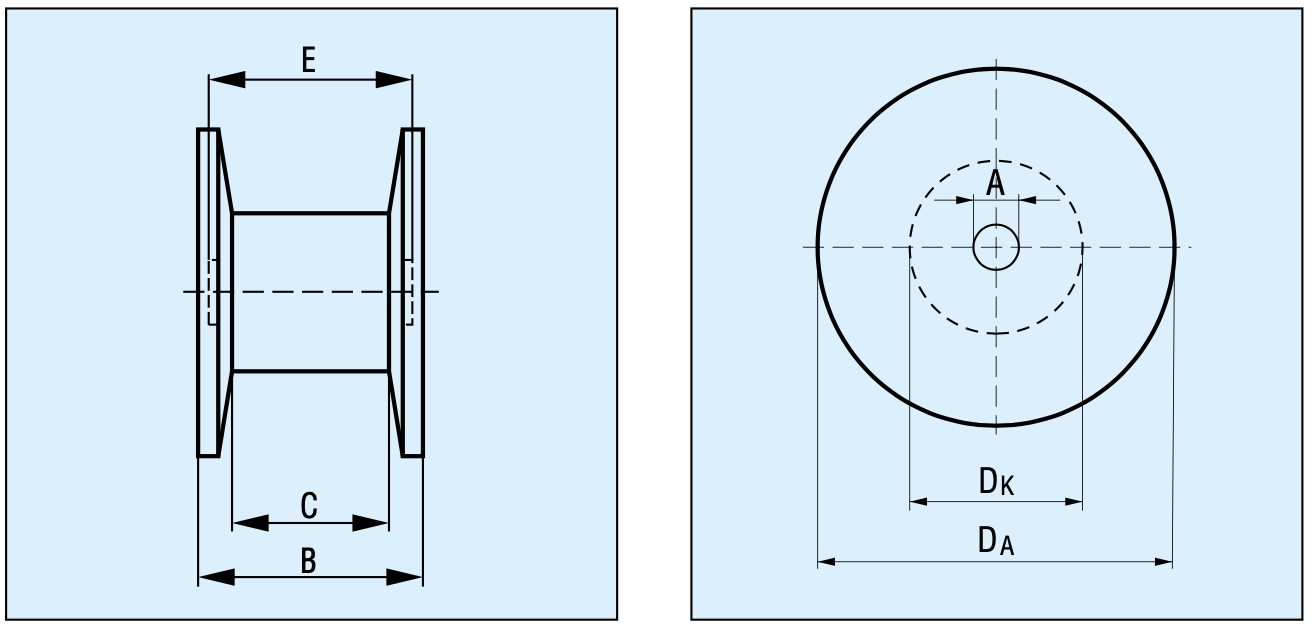
  • D_e: Cable outer diameter (mm).
  • D_flange: (DA): Drum flange outer diameter (mm).
  • D_core: (DK): Drum core / barrel diameter (mm).
  • D_bore (A): Bore diameter (mm) used for the drum drawing/spec.
  • D_wheel (E): Inner width / wheel dimension (mm) used for the drum drawing/spec.
  • w_drum (B): Overall drum width (mm).
  • w_wind (C): Usable winding width between flanges (mm).
  • d_free: Free clearance margin (mm). This keeps cable away from the flanges/core limits.
  • method: Filling method (string), e.g. "wild", "full", or another mode.

Step 1: Calculate how many layers and windings fit

  • Number of radial layers (num_layers) is computed from the free radial space:
    • Available radial thickness is (D_flange - D_core - 2 * d_free) / 2 (mm). This is because diameters are converted to radius by dividing by 2, and clearance is applied on both sides.
    • Dividing that thickness by D_e gives the number of cable layers that fit radially.
    • floor(...) ensures the result is an integer that does not exceed the available space.
  • Number of windings across the width (num_windings) is: floor(w_wind / D_e). This is how many cables of diameter D_e fit side-by-side within the usable winding width.

Step 2: Calculate cable length for the selected filling method

The code proceeds only if num_layers > 0 (at least one radial layer fits). The length calculation uses a simplified model:

  • The effective average diameter for winding is approximated as: D_core + num_layers * D_e (mm). (This represents winding on top of the core and building up by num_layers layers.)
  • One winding turn length is approximately π × diameter.
  • Total turns are approximated as num_layers × num_windings.
  • Division by 1000 converts from millimeters to meters.
Method 1: wild
  • L_cable is multiplied by 0.92 to account for imperfect packing (random/wild winding does not fill space as efficiently).
  • space_w = 0 because the model assumes the usable width is effectively consumed by the winding behavior.
Method 2: full (LV cable)
  • Uses the full packing length (no 0.92 factor).
  • Remaining width clearance is computed as: space_w = w_wind - num_windings * D_e (mm).
Method 3: else Decrease by one winding (MV/HV cable)
  • Decreases num_windings by 1 before computing the length. This models leaving one winding “column” empty (for example, due to practical constraints).
  • Remaining width is then: space_w = w_wind - num_windings * D_e (mm).

Step 3: Remaining radial space

After placing num_layers layers radially, the unused radial clearance is:

space_r = (D_flange - D_core - 2 * num_layers * D_e) / 2 (mm).

This is the leftover distance (in radius) between the outermost cable layer and the flange limit.

Outputs produced by this snippet

  • num_layers: Number of cable layers that fit radially (integer).
  • num_windings: Number of windings that fit across the width (integer, possibly reduced by 1 in fallback mode).
  • L_cable: Estimated total cable length that fits on the drum (meters).
  • space_w: Remaining unused winding width (mm).
  • space_r: Remaining unused radial space (mm).

Example

Let us run a simple example with following inputs using the method 3 with decrease by one winding:

Cable drum inputs

Electrical fieldPreview in editor
Cable drum sideview
 Cable drum front view

The calculation returns the following results:

Cable drum results

References

The data for a list of empty drums is taken from the 'Manual for Transportation and Cable Laying' by Brugg Cables.

Cable drum inputs

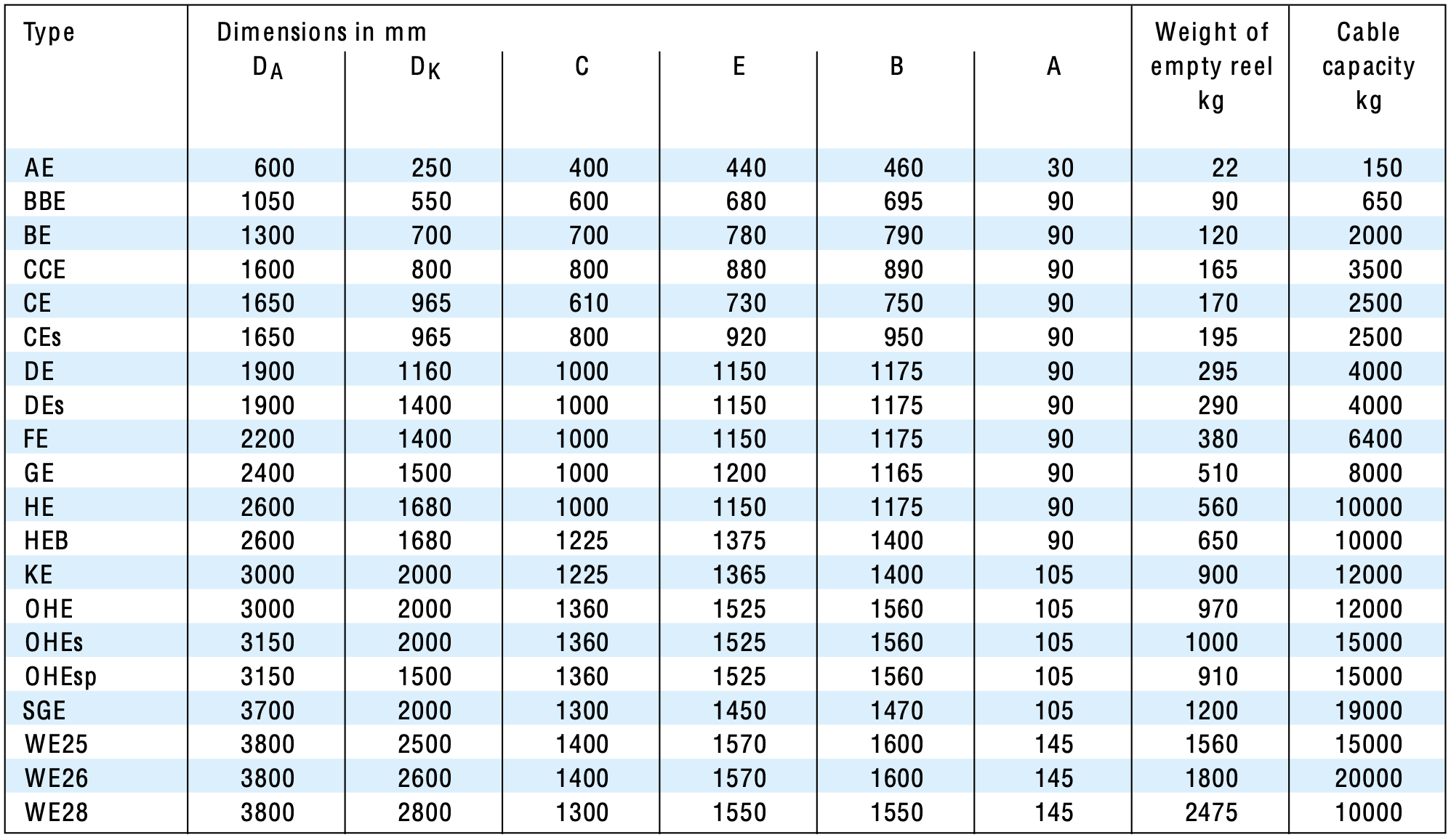
Cable drum table from Brugg Cables

From this data we created a function to calculate the weight of a drum with any dimension up to a flange diameter of 5 m using a 5th degree polynominal best-fit including the min and max envelopes. The problem is that depending on the actual design of the drum and the ratio between core to flange diameter as well as the width there are jumps in the data.

Polynominal envelopesActual vs predicted valuesExtrapolation
Cable drum polynominal envelopes
 Cable drum actual vs predicted values
 Cable drum extrapolation

 

Categories
41
26
34
19
9
22
16
Archive
6
9
2
3
11
24
11
9
10
2
9
11
2