The electric field calculator can calculate and visualize the electrical field stress and the voltage gradient within the insulation.
Posted 2026-01-03
Categories:
Tools
We provide you with a tool to calculate the electrical field within the cable insulation.
The value of the voltage gradient at point x within the insulation can be calculated using a logarithmic relationship. The electrical field strength is highest above the conductor shield (inner semi-conducting layer), below the insulation and lowest below the insulation screen (outer semi-conducting layer), above the insulation.
The electrical field strength can be calculated using following logarithmic relationship:
$$E_i = U_e \cdot \frac{1}{r_x \ln\left(\frac{r_{osc}}{r_{isc}}\right)} = \frac{\delta_i U_e \left(\frac{r_x}{r_{osc}}\right)^{\delta_i - 1}}{r_{osc} \left(1 - \left(\frac{r_{isc}}{r_{osc}}\right)^{\delta_i}\right)}$$The radius above the inner semi-conducting layer $r_{isc}$ [mm] and the radius over capacitive insulation layers $r_{osc}$ [mm] are defined as:
$$r_{isc} = D_c / 2 + t_{cs}$$ $$r_{osc} = D_i / 2$$with $D_c$ being the diameter of the conductor, $t_{sc}$ being the thickness of the conductor shield (including any tapes around the conductor), $D_i$ being the diameter over the insulation without the insulation screen $t_{is}$.
The vacuum permittivity or electric constant $\epsilon_0$ [F/m] is a physical constant for the capability of the vacuum to permit electric field lines. It has a value of around 8.85 $\cdot 10^{-3}$. With the relative permittivity of the insulation material $\epsilon_i$ the capacitance $C_b$ [F/m] of the insulation can be calculated.
With the system frequency $f$ the circular frequency $\omega$ $= 2 \pi \cdot f$ [Hz] is calculated.
When we define the geometric factor $f_{log}$ we can write simple equations for the capacitance in [F/m] and the maximal and minimal value of the electrical stress in the insulation in kV/mm with the electrical field strength being proportional to the line-to-ground voltage $U_e$.
$$f_{log} = \ln\left(\frac{r_{osc}}{r_{isc}}\right)$$ $$C_b = \frac{2\pi \epsilon_0 \epsilon_i}{f_{log}}$$ $$E_{max} = U_e \cdot \left(\frac{1}{r_{isc}}\right)$$ $$E_{min} = U_e \cdot \left(\frac{1}{r_{osc}}\right)$$We model an example cable as follows:
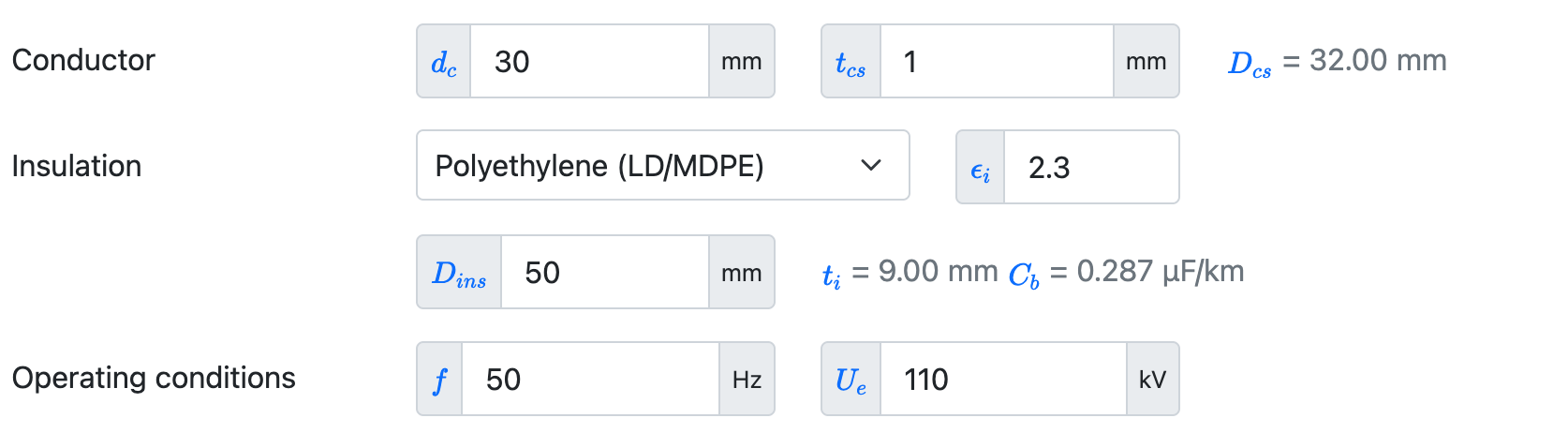
The resulting electrical field is shown:
| Electrical field | Electrical field strength and voltage |
|---|---|
 |
 |