Twisting cables reduces the magnetic field because the current direction alternates along the cable length, causing the individual magnetic fields to partially cancel each other out. Our tool can calculate this effect depending on how much the cable is twisted.
Posted 2026-01-04
Categories:
Tools
The electric field is completely shielded by the cable sheath and the soil. This means that no electric field is detectable even if we are standing directly above the underground cables. The magnetic fields, however, freely penetrate practically all materials, and screening is therefore only possible with the aid of special metal alloys and even then only to a limited extent.
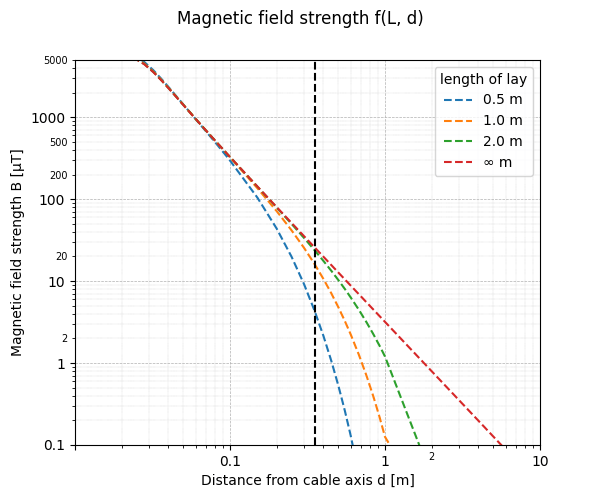
We provide you with a tool to calculate the magnetic field of twisted cables with which you can see the reduction of the magnetic field depending on the length of lay at a specific point of observation.
The magnetic field is calculated based on the law of Biot-Savart where each sub-conductor is represented by a filament current extending along its axis. The strength of a magnetic field is proportional to the current and decreases as the distance from the source increases. It is not stopped by ground or buildings, trees, etc. The magnetic fields from different phases may tend to add together or cancel each other depending upon location of the phases and the direction of the load flow.
Twisting cables reduces the magnetic field because the current direction alternates along the cable length, causing the individual magnetic fields to partially cancel each other out. By twisting, the opposing fields are more evenly distributed and destructively interfere, significantly reducing the net external magnetic field.
The magnetic field strength is calculated at any point due to all current sources basically as it was explained in an old post on our blog.
For the calculation with twisted cables we require some input parameters such as the system frequency $f$ from which the circular frequency $\omega$ $= 2 \pi \cdot f$ [Hz] is calculated. The conductor current $I_c$ [A] is required and from it the complex phase currents are defined using the phase angles 1, -0.5 - j0.866, -0.5 + j0.866:
The twisted cables are being calculated over a distance of 60 m with $z = -30 ... +30$ m and in steps of $\delta_z = 0.01$ m, with the observation point at $z = 0$ and distance $d_{xy}$ [mm] to the center of the twisted cables in directions x and y.
The calculation is possible for multi-core cables where the inner cores are twisted as well as for twisted single-core cables. We need to calculate the radius of the incircle as well as the radius of the bundle.
We calculate the average radius $r_m$ and the and the twist angle per meter $\phi_j$ with the following two equations:
| $$r_m = r\,\frac{1+\dfrac{1}{\cos\!\left(\pi\,\dfrac{\delta_r}{L_{\mathrm{lay}}}\right)}}{2}$$ |
| $$\phi_j=\frac{2\pi}{L_{\mathrm{lay}}}$$ |
The length of lay $L_{lay}$ [mm] defines the reduction in magentic field strength – the shorter $L_{lay}$ is, the smaller the resulting magnetic field will be. Of course, the length of lay must still be physically possible to make sense.
The actual iterative calculation steps are quite tricky and we cannot explain them adequately in a simple blog post. Also we don't want to provide the means for our competitor from Down Under to simply copy once more something we developed with great difficulty.
We model an example cable as follows:
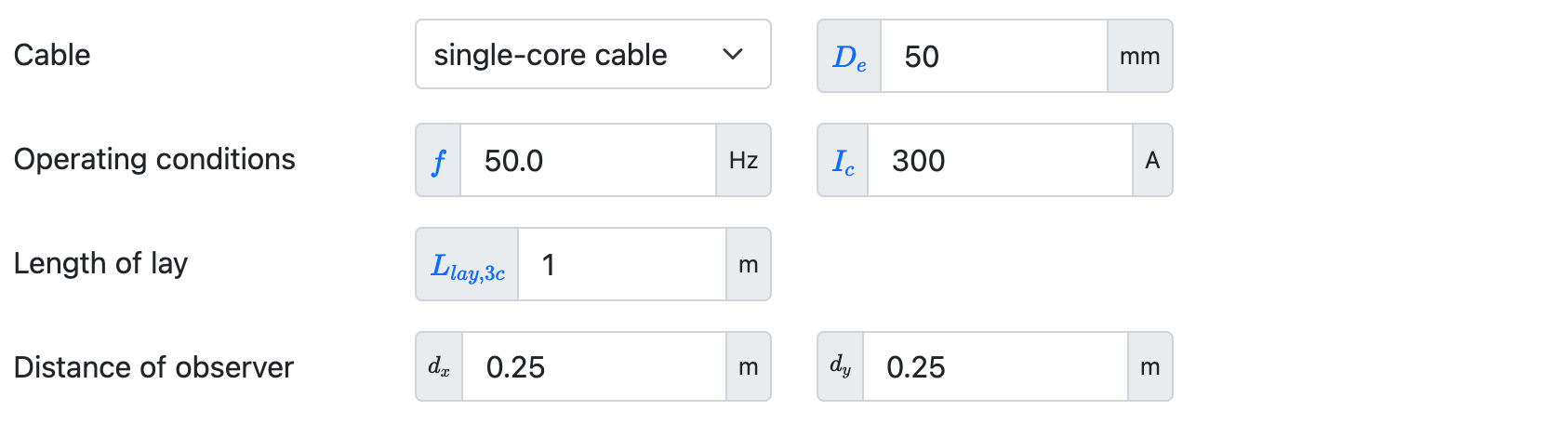
The calculated magnetic field strength at the point of observation is 15.9 µT:
The visualization of the twisted cables is shown in the two following representations:
| Elongation of the cables along z-axis | Position of the three cable conductors in 3D |
|---|---|
 |
 |
The effect of the twisting, depending on the length of lay, can be seen in the following plot. Please note that both axes are logarithmic which signifies that the reduction is very substantial with two to three orders of magnitude.