Interpretation and generalization of the calculation of the thermal resistances of the constituent parts of multi-core cables, as defined in IEC 60287-2-1.
Posted 2015-03-27
Categories: Theory
This content is outdated! Please refer to the new posts about three-core cables No 1 and No 2.
This blog post discusses the general approach used in Cableizer in order to calculate the thermal resistance between one conductor and the sheath $T_1$, the thermal resistance between the sheath and the armour $T_2$, and the thermal resistance of the outer sheath $T_3$ of multi-core cables.
Two different isothermal surfaces can be found in a cable: A metallic sheath or tape screen, and an armour. A wire screen is not considered to be enough to create an isothermal. The sheath or tape screen can be around each individual phase (SL-type), or it can be common to all phases. All in all, the following five cable configurations should be treated accordingly:
| $T_1$ | As for a single core-cable (4.1.2.1). $t_1$ is the distance from the conductor surface to the inside of the tape screen (tape screens present, but no sheaths), the inside of the sheath (sheaths present, but no tape screens), or the inside of the tape screen plus half the screen serving thickness (both tape screens and sheaths present). When the sheaths are corrugated, half the corrugation depth is added as well. |
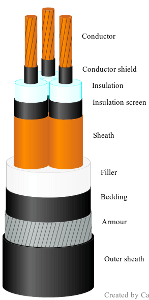 |
| $T_2$ | As for an SL-type cable (4.1.3.2). $t_2$ is the distance between the sheath/tape screen and the armour, including the filler thickness. The outside of the sheath/tape screen corresponds to the outside of the tape screen when there is no sheath, to the outside of the sheath when there is no tape screen, or to the outside of the sheath minus half the screen serving thickness when both tape screens and sheaths are present. Again, when the sheaths are corrugated, half the corrugation depth is subtracted as well. The geometric factor $G_2$ is based on $t_2$, expressed as a fraction of the outer diameter of the sheath or tape screen. If the sheaths or tape screens are touching, the upper curve is used for the calculation of $G_2$, otherwise the lower curve. |
|
| $T_3$ | General case (4.1.4.1). $t_3$ is the thickness of the outer sheath. |
| $T_1$ | As for a single core-cable (4.1.2.1), identical to case 1) above. |  |
| $T_2$ | 0, included in $T_3$. | |
| $T_3$ | Special case (4.1.4.2). The external diameter of the armour used in the general case is replaced with the diameter over the filler/binder tape. The geometric factor $G_2$ is calculated analogous to case 1) above. |
| $T_1$ | Special case considering the screening factor $K$ (4.1.2.3). As opposed to the standard, the screening factor is also applied to two-core cables. $t_1$ is calculated in the same way as in case 1) above, but will now contain the filler thickness as well. The geometric factor $G_1$ is calculated as a function of $t_1$, depending on the number and shapes of cores. |
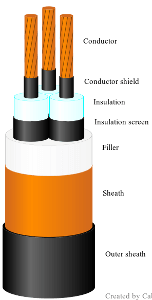 |
| $T_2$ | General case (4.1.3.1). $t_2$ is calculated in the same way as in case 1) above, but does not contain the filler thickness. |
|
| $T_3$ | General case (4.1.4.1), identical to case 1) above. |
| $T_1$ | As for belted cables (4.1.2.2). $t_1$ is the distance from the conductor surface to the inside of the armour bedding. The geometric factor $G_1$ is calculated identical to case 3) above. |
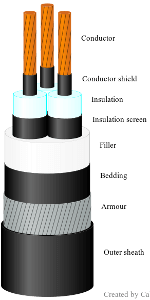 |
| $T_2$ | General case (4.1.3.1). $t_2$ is the thickness of the armour bedding. |
|
| $T_3$ | General case (4.1.4.1), identical to case 1) above. |
| $T_1$ | As for belted cables (4.1.2.2). $t_1$ is the distance from the conductor surface to the inside of the outer sheath. The geometric factor $G_1$ is calculated identical to case 3) above. |
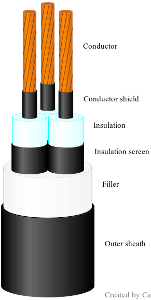 |
| $T_2$ | 0, included in $T_1$. | |
| $T_3$ | General case (4.1.4.1), identical to case 1) above. |