Cableizer
Log in

Validation of emergency rating calculations acc. IEC 60853-2

The emergency rating calculations have now been updated and validated according to IEC standard 60853-2.

Posted 2019-10-01
Categories: Theory, Validation

Emergency rating calculation method

Transient emergency rating calculations are coverer in section four (chapter 8) of the IEC standard 60853-2. The method for calculating the emergency ratings applies to cables buried in the ground, either directly or in ducts, and to cables in air. The method is intended for emergency loads not greater than 2.5 times their rated full load current $I_R$ (100% load factor).

The procedure for calculating the short time emergency rating is based on the knowledge of the conductor temperature transient of a cable circuit carrying a constant current $I_1$ (applied for a sufficiently long time for steady-state conditions to be reached) being subjected to an emergency load current $I_2$ (greater than $I_1$). If $I_2$ is applied for a certain duration, the question is how large may $I_2$ be so that conductor temperature does not exceed a specified maximum permissible temperature $θ_{max}$, taking into account the variation of the electrical resistivity of the conductor with temperature.

$$I_2 = I_R \sqrt{ \frac{(R_R/R_{max})(r-h_1^2[R_1/R_R])}{θ_R(t)/θ_R(∞)} + \frac{h_1^2R_1}{R_{max}} }$$

The above equation (8-1) for the calculation of the emergency current $I_2$ from the IEC standard 60853-2 has been interpreted and clarified in Cableizer as follows:

  • $r=θ_{max}/θ_R(∞)=1$, since the maximum permissible temperature rise above ambient at the end of the period of emergency loading $θ_{max}$ in Cableizer is always equal to the value of $θ_R$ in the steady-state $θ_R(∞)$.
  • $R_R=R_{max}$, since the a.c. resistance $R_R$ of the conductor with sustained application of rated current $I_R$ in Cableizer is always equal to the a.c. resistance $R_{max}$ of the conductor at the end of the period of emergency loading.
With the above, equation (8-1) becomes:

$$I_2 = I_{\mathrm{R}} \sqrt{\frac{\Delta \theta_{\mathrm{R_{\mathrm{\infty}}}}}{\Delta \theta_{\mathrm{t}}} \left(1 - \frac{h_{\mathrm{1}}^{2} R_{\mathrm{1}}}{R_{\mathrm{max}}}\right) + \frac{h_{\mathrm{1}}^{2} R_{\mathrm{1}}}{R_{\mathrm{max}}}}$$

Verification

The following results show a good agreement between Cableizer and example F6 from the IEC standard 60853-2:

CableizerIEC 60853-2
Steady-state current before emergency transient $I_1$1195 A1195 A
Transient conductor current $I_R$1555.4 A1550 A
6 hours emergency load current $I_2$2083.4 A2131 A

The following two figures show the permissible emergency load currents for different emergency durations in the range from 10 minutes up to 36 hours.

  • On the left, the maximum permissible conductor temperature $θ_{max}$ is 85 °C as in example F6 above. It can be noticed that the emergency rating current for 10 minutes is exceeding the limit of 2.5 $I_R$, which means that this result should only be used after careful consideration and under close supervision.
  • On the right, $θ_{max}$ ist 62 °C, just slightly above the steady-state temperature before the emergency period of 61.1 °C. As expected, emergency load currents are very limited in this scenario since the cable is already operating close to its thermal limit.

$θ_{max}$ = 85 °C$θ_{max}$ = 62 °C
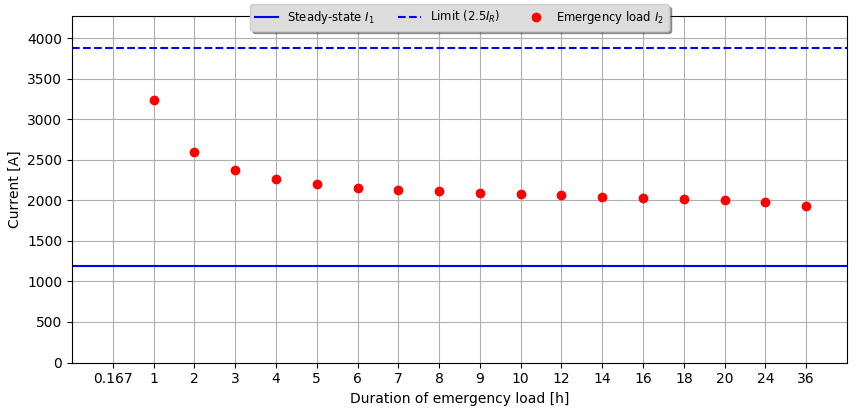Emergency load currents at 85C

Limitations

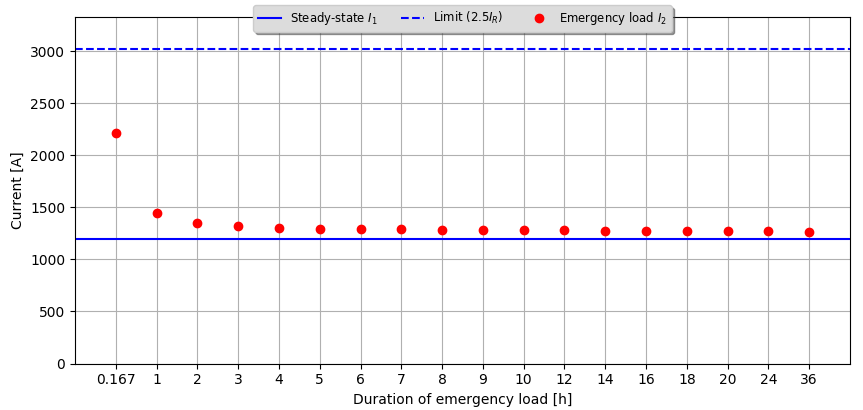In Cableizer, the emergency rating can only be calculated for a single cable system at a time. The thermal effect of the emergency loading on nearby cable systems is not considered either. In case nearby cable systems are already operated at or close to their thermal limit, the emergency load current calculated in Cableizer might be too large and could harm nearby cable systems.

 

Categories
8
44
8
25
8
18
11
Archive
3
12
24
10
9
10
2
9
11
2