With the increasing number and scale of photovoltaic power plants and their cyclic nature of power generation, accurate cable rating calculations become essential in order to optimize their capacity. This blog post discusses the underlying basic theory, the applicable standards, and their implementation in the web-based cable rating software Cableizer.
Posted 2019-03-13
Categories: Theory
An important aspect during the development of ground-mounted PV (Photovoltaic) power plants is the planning of LV (Low Voltage, up to 1 kV) and MV (Medium Voltage, above 1 kV up to 36 kV) cable systems. Cable rating calculations are an essential part of this planning, especially when multiple parallel cable systems are to be laid underground. For these calculations, many project developers rely on the international cable calculation software Cableizer, developed and distributed by Braavos GmbH from Switzerland.
The cable rating calculation methods used in the software Cableizer are based on verified mathematical methods as published in international standards and technical publications. In the following blog post we present you with some technical details, capabilities and limitations of these methods.
In addition, some explanations are given with respect to the planning of cable systems for large-scale ground-mounted PV power plants.
There are a number of different methods and procedures that can be used to calculate the current rating of a cable system. Likewise, there are many standards, reports and technical papers that give methods for the calculation of current ratings but no one document gives methods for all situations. In some situations there is more than one calculation method published.
Most underground cable ratings calculated using analytical methods are evaluated based on the fundamental concept of heat transfer through a solid medium by thermal conduction. An equivalent thermal circuit consists of heat loads, thermal resistances, and thermal capacitances. It is developed to model a specific cable construction and its surrounding. A temperature rise results from the heat flow through the thermal resistances and capacitances. The thermal capacitance introduces a delay in the response of the temperature to changing loads.
| Thermal resistance (left) and thermal capacitance (right) [1] |
|---|
 |
The cable system can be subjected to a number of different loading patterns, where the current can vary over a period of time. Typical calculation methods assume that the temperatures of the cable have reached steady-state conditions after a long period of continuous operation and this load pattern is known as continuous rating. For this loading pattern only the heat generated, the thermal resistances of the system and the constraining temperatures need to be considered. The thermal capacitances of each part of the cable system can be neglected.
| Steady-state thermal model [2] |
|---|
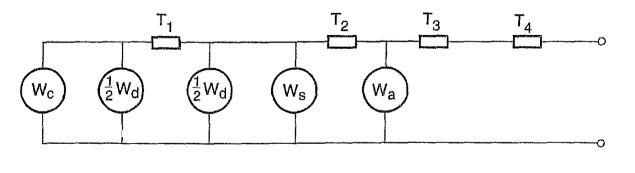 |
The temperature rise above ambient temperature is obtained as [5]:
| $\Delta \theta = \left( I^2R+W_d/2 \right) T_1 + \left( I^2R (1+\lambda_1) + W_d \right) n T_2 + \left(I^2 R (1+\lambda_1+\lambda_2) + W_d \right) n (T_3+T_4)$ |
The thermal model leads to the equation to calculate the permissible current rating described in the groundbreaking paper by Neher/McGrath [3] which can be found in IEC 60287-1-1 [5]:
| $I = \left( \frac{\Delta\theta-W_d\left( T_1/2+n(T_2+T_3+T_4)\right)}{RT_1+nR(1+\lambda_1)T_2+nR(1+\lambda_1+\lambda_2)(T_3+T_4)}\right) ^{0.5}$ |
Various loading scenarios other than continuous 100% loading may be considered in situations where the thermal capacitances of the cable system, including the thermal environment, are factored into the rating calculations. Two general methods may be used to analyze time varying loadings: either numerical or analytical.
Numerical methods include the finite elements method or finite difference method. Analytical methods include the method published by Neher/McGrath [3] for cyclic ratings and the methods in IEC 60853 [6] that can be used in a number of different loading patterns.
After a 100% (constant) load pattern, the most fundamental loading scenario to consider is an indefinitely repeated load pattern. This type of evaluation considers the long thermal time constant of the earth surrounding the power cable system and recognizes that the extent of heating that occurs in the soil will effectively be the average of the heat generated by the power cable during the load cycle. In practice, loading patterns vary, but a common load variation that has some consistency is usually associated with a 24-hour load cycle.
The load factor ${LF}$ is generally defined as the ratio of average load over a period of time compared to the maximum load over the same period of time. With known load values (e.g. recorded power), ${LF}$ may be calculated:
| $LF = \frac{\sum^{24}_{i=1} P_i}{24 P_{max}}$ |
For cable rating purposes, the heat output (or losses) emitting from the cable must be considered, so the ratio of average losses to peak losses must be known; the loss factor $\mu$ can be calculated:
| $\mu = \frac{1}{W_{max}\tau} \int^{\tau}_{t=0} W(t) dt \cong \frac{\sum^{24}_{i=1} I_i^2}{24 I_{max}^2}$ |
System planners may be able to offer a loss factor but may not know the actual (or projected) loading for a cable circuit. Empirical relationships such as the following, using a load loss constant coefficient $k_{LF}$ , may be used to relate the loss factor to the load factor:
| $\mu = k_{LF}{LF}+{LF}^2(1-k_{LF})$ |
Neher/McGrath [3] proposed a value of 0.3 for $k_{LF}$ resulting in:
| $\mu = 0.3{LF}+0.7{LF}^2$ |
There are two analytic approaches considering the cyclic loading pattern. The calculation procedures in IEC 60287 [5] may be modified in one of two ways:
The IEC 60853-1 [6] chapter 3 in part 1 and section 3 in part 2 give a cyclic rating factor $M$ with a value greater than or equal to 1.0 in order to consider the cycle nature of the load. The method supports considering cyclic ratings for periods of 24 hours or other durations. The method requires that some knowledge of the time at peak current be known in developing the factors (or assumptions as in Neher/McGrath [3] can be made if these are not known).
Neher/McGrath [3] offered an alternative method for considering cyclic loading by making an assumption that the 24-hour load cycle closely followed a sinusoidal load shape. On this basis, peak losses are applied to cable components and the portion of the earth thermal circuit that is “near” to the cable, while average daily (24-hour cycle) losses are applied to the thermal resistance values of the ground beyond a characteristic diameter $D_x$. $D_x$ is determined based on the thermal diffusivity of the soil and is typically taken to be about 212 mm for most soils and regardless of the outer diameter of the cable, conduit or pipe. The earth thermal resistance is then determined using an equation of the form as presented in [3]:
| $T_4 = \frac{\rho_{Fill}}{2\pi} \left( \ln{\frac{D_x}{D_{earth}}} + {\mu}\left( \ln{\frac{2L+\sqrt{4L^2-D_x^2}}{D_x}} + \ln{F} \right) \right) + {\mu}\frac{N}{2\pi}(\rho_{Native}-\rho_{Fill}){G_b}$ |
The above methods for calculating cyclic ratings should only be considered for the buried portions of cable systems. For cables in tunnels, air, water or other non-solids, transient ratings are more complex. Cable systems with segments in free air will generally have a much shorter thermal time constant and, therefore, considerations of cyclic rating for cables in air are generally not made.
Cableizer is a software package for the design of power cable systems using electrical, mechanical, thermal and environmental calculations. The software is web-based which allows its usage on any operating system like Windows, Mac, or Linux. Cableizer also works on any device with internet connection like your computer, tablet or mobile phone.
For thermal cable rating, Cableizer uses methods from international standards with numerous extensions:
Regarding buried cables, the software allows the calculation of up to 16 parallel systems with different cable design, laying arrangement, current loading, and frequency.
The calculation of transient current steps, emergency rating, or cyclic ratings according to IEC 60853 [6] is limited to one system only. But a separate load factor acc. Neher/McGrath may be applied for each system plus the user has the possibility to change the time period.
In the majority of practical cases, the load variation will show a more complex pattern than can be described with a daily load factor. For example, loading of cables is usually much lighter during the weekend than during the weekdays. And for deeply buried cables, the yearly load variations will play a significant role because of the mentioned long time constants at great depths. Cableizer offers the possibility to add a weekly load factor and a yearly load factor for each system.
In August 2018, the IEC published a new international technical specification IEC TS 62738 [8]. This document sets out general guidelines and recommendations for the design and installation of utility scale ground-mounted PV power plants.
A PV power plant is defined within this document as a grid-connected, ground-mounted system comprising multiple PV arrays and interconnected directly to a utility’s medium voltage or high voltage grid. Technical areas addressed are those that largely distinguish PV power plants from smaller, more conventional installations, including ground mounted array configurations, cable routing methods, cable selection, overcurrent protection strategies, equipotential bonding over large geographical areas, and equipment considerations.
In chapter 7.3.4.9.1, the specification further states that for cables in trenches, whether in ducts or direct-buried, site specific solar output load profiles may be used in place of 100 % load factor assumptions to determine effective loading criteria, using methods described in IEC 60853 [6], all parts, or similar methods.
In chapter 7.3.4.1 of IEC TS 62738 [8], the specification states that the above and below-ground cables should incorporate de-rating factors associated with spacing and soil thermal resistivity calculations in accordance with IEC 60364-5-52 [7].
The standard IEC 60364-5-52 [7] provides tables with the current-carrying capacities in amperes under continuous load (steady-state) for different cable cross sections and different methods of installation under certain standard conditions.
Standard conditions for XLPE cables for example are a maximal permissible conductor temperature of 90°C and an ambient temperature of 30°C in air or 20°C in ground. The standard also provides tables with correction factors, known as de-rating factors, for deviations to the standard conditions. This may be for example higher or lower ambient temperatures, grouping of cables (of same type and identical load), different soil thermal resistivity or other parameters. The use of the standard IEC 60364-5-52 [7] for current-carrying capacities is limited to the standard laying configurations under standard conditions as covered by the standard.
There are multiple other standards such as VDE, IEEE, NEC which provide similar tables with standard current-carrying capacities and de-rating factors and may be used equivalently.
The ampere values given in IEC 60364-5-52 [7] had been calculated for a typical cable design using the methods according to IEC 60287 [5] which is the international standard which defines the procedures and equations to be used in determining the current carry capacity of cable under continuous load (100% load factor). The standard is applicable to all AC voltages and DC cables up to 5 kV.
The method used in the IEC 60287 [5] is based on the calculations published in Neher/McGrath [3] which considered the heat transfer issues associated with underground system ampacities. Many of ampacity calculations we use today are based on Neher/McGrath [3]. Later work by CIGRE [4] documented an ampacity procedure into the international standards IEC 60287 [5] and IEC 60853 that provides a step-wise approach to calculating ampacity based upon cable construction.
The IEC 60364-5-52 [7] states, that the appropriate values of current-carrying capacity may also be determined as described in the IEC 60287 [5] series directly. As the IEC 60287 [5] is based on Neher/McGrath [3], this method may be applied likewise.
The IEC 60287 [5] provides a set of equations to calculate the current rating with a 100% load factor. For rating with a load factor smaller than 100%, the analytical methods published by Neher/McGrath for cyclic ratings [3] and the methods in IEC 60853 [6] can be used in a number of different loading patterns. The two calculation approaches give similar results, although their treatment of daily load cycles is different.
Neher/McGrath [3] assumes a sinusoidal load shape and uses a 24-hour loss factor to account for an overall “averaging” effect of heat output from the cable beyond a certain diameter. Within this diameter, the temperature rise across the thermal resistances in the cable and nearby soil is proportional to the peak heat output from the cable. At distances greater than this diameter away from the cable center, the temperature rise is proportional to the average daily heat output.
The methods in the IEC 60853 [6] require only a knowledge of the full shape of the load variation for not more than 6 h immediately preceding the time of maximum temperature and an average value for times before that. The cyclic rating factor is designated by the letter $M$, and represents the factor by which the permissible continuous current rating (100% load factor) can be multiplied to obtain the peak current during a daily cycle, such that during this cycle, the conductor reaches, but does not exceed, the standard maximum permissible temperature.
The method according Neher/McGrath [3] provides the advantage that the calculated loss factor $\mu$ can be directly integrated into the equation for the current rating. This allows for calculation of multiple parallel cable systems with different loading and load cycles. In comparison, the use of IEC 60853 [6] is rather cumbersome, especially when dealing with multiple parallel cable systems.
| [1] | Elements of Thermal Systems, lpsa.swarthmore.edu/Systems/Thermal/SysThermalElem.html, 2018 |
| [2] | G. Anders, “Rating of Electric Power Cables”, 1997 |
| [3] | J.H. Neher and M.H. McGrath, “The Calculation of the Temperature Rise and Load Capability of Cable Systems”, 1957 |
| [4] | CIGRE Guide 640 “A Guide for Rating Calculations of Insulated Cables”, 2015 |
| [5] | IEC 60287, “Electric cables – Calculation of the current rating” Part 1-1 “Current rating equations (100 % load factor) and calculation of losses – General“, 2014 Part 2-1 “Thermal resistance – Calculation of thermal resistance“, 2015 Part 2-2 “Thermal resistance – A method for calculating reduction factors for groups of cables in free air, protected from solar radiation”, 1995 Part 2-3 “Thermal resistance – Cables installed in ventilated tunnels”, 2017 Part 3-3 “Sections on operating conditions – Cables crossing external heat sources”, 2007 |
| [6] | IEC 60853, “Calculation of the cyclic and emergency current rating of cables” Part 1: “Cyclic rating factor for cables up to and including 18/30 (36) kV”, 1985 Part 2: “Cyclic rating of cables greater than 18/30 (36) kV and emergency ratings for cables of all voltages, 1989 |
| [7] | IEC 60364-5-52, “Low-voltage electrical installations – Part 5-52: Selection and erection of electrical equipment – Wiring systems”, 2009 |
| [8] | IEC TS 62738, “Ground-mounted photovoltaic power plants – Design guidelines and recommendations”, 2018 |